Çan eğrisi, istatistikte ve veri analizinde kullanılan bir grafik türüdür. Çan eğrisi, bir veri kümesinin dağılımını görsel olarak göstermek için kullanılır. Genellikle, veri noktalarının yoğunluğunu ve ortalamasını gösterir. Çan eğrisi ayrıca “normal dağılım” veya “Gauss eğrisi” olarak da adlandırılır, çünkü normal dağılımı temsil eder.
Çan eğrisini çizmek için aşağıdaki adımları izleyebilirsiniz:
- Veri Toplama: İlk adım, analiz yapmak istediğiniz veriyi toplamaktır. Bu veri, bir özellik veya olayın örneklerini içerebilir. Örneğin, bir sınıftaki öğrencilerin notlarını incelemek istiyorsanız, bu öğrencilerin notlarını toplamalısınız.
- Veriyi İnceleme: Veriyi inceleyerek temel istatistiksel özellikleri belirleyin. Bu özellikler arasında ortalama, standart sapma ve varyans bulunabilir. Bu özellikler, çan eğrisini çizerken kullanılacaktır.
- Çan Eğrisi İçin Olasılık Yoğunluk Fonksiyonunu Hesaplama: Normal dağılım için olasılık yoğunluk fonksiyonunu hesaplamak gereklidir. Bu fonksiyon, her veri noktasının belirli bir değere düşme olasılığını gösterir. İşte bu fonksiyonun bir örneği:
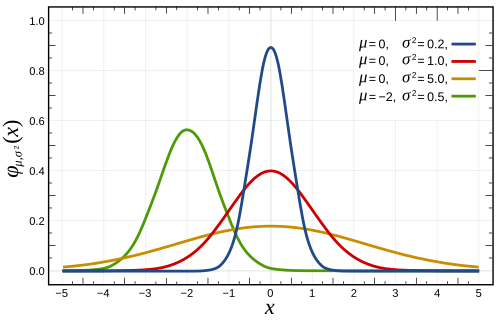
Bu fonksiyon, μ (ortalama) ve σ (standart sapma) gibi istatistiksel parametrelerle tanımlanır.
- Çan Eğrisini Çizme: Şimdi, hesaplanan olasılık yoğunluk fonksiyonunu kullanarak çan eğrisini çizebilirsiniz. Bu çizimde, x-ekseni veri değerlerini, y-ekseni ise bu değerlerin olasılıklarını temsil eder. Çan eğrisi, ortalama etrafında simetrik bir şekilde yükselir ve dağılımın ne kadar yayıldığını (standart sapma ile ölçülür) gösterir.
- Veriyi Karşılaştırma: Çan eğrisini çizdikten sonra, veri kümenizin bu eğriye ne kadar uygun olduğunu değerlendirebilirsiniz. Verileriniz normal dağılıma ne kadar yakınsa, çan eğrisi o kadar iyi uyar.
Çan eğrisi, veri analizi, hipotez testi ve tahmin yapma gibi istatistiksel işlemlerde sıkça kullanılır. Verilerinizin normal dağılıma uyması durumunda, istatistiksel analizlerde daha fazla kullanabileceğiniz bir temel oluşturabilir. Ancak, veriler normal dağılıma uymuyorsa, farklı istatistiksel yöntemlere başvurmanız gerekebilir.
